Aries: An LSI Macro-Block for DSP Applications
![[PREV]](PIC/back.gif)
![[TOC]](PIC/toc.gif)
![[NEXT]](PIC/fwd.gif)
![[PREV]](PIC/back.gif)
![[TOC]](PIC/toc.gif)
![[NEXT]](PIC/fwd.gif)
Throughout the entire science history man has tried to understand, analyze, imitate and most of all, control its surrounding environment. The limits of human capabilities were the dominant factorsfor most of the technical inventions. They felt cold, understood that fire would provide the necessary heat and then they went on to generate fire and control it. There are many key inventions that has had a key role in the history of civilization: the wheel, the invention of writing, bronze, gunpowder, the steam engine and integrated circuits have all changed the way of life dramatically. Today, thanks to the extended usage of integrated circuits, we are said to be living in an information age.
A very important breakthrough in information processing came with the introduction of integrated digital circuits. Digital circuits, unlike their analog counterparts, interpret their inputs as one of two logic states: logic "1" and logic "0". The output of any digital circuit comprises of a set of these states. These two states are enough to define a binary number system where any mathematical operation can be realized, which makes digital circuits ideal candidates for computational operations. Furthermore digital information is much more noise immune than analog signals and there are practically lossless methods to store digital states. There is only one slight problem:
Every piece of natural information is strictly analog in nature: they consist of continuous signals. Fortunately it is quite easy to express any analog value in terms of a number of digital states. Analog to Digital Converter (ADC) circuits are used to make this conversion. The digital circuits can then process, store and manipulate these analog signals. Once a result is available Digital to Analog Converter (DAC) circuits can convert the digital value into an analog signal.
Digital Signal Processing, is a general term that describes specialized algorithms for signal processing using digital circuits. These signals can range from low frequency audio signals to high resolution image image signals. Most DSP applications can be described as various filtering algorithms to enhance the original signal. Applications include:
Especially new multimedia applications and standarts (eg. MPEG2, MPEG4) require computation-intensive transformations to reduce the bandwidth and to enhance the quality of audio and video signals.
![[TOC]](PIC/toc.gif)
![[TOP]](PIC/up.gif)
The basic digital unit is called a bit. One bit can only have one of the two values: logic "0" or logic "1" (commonly referred to as 0 and 1). It is evident that one bit alone can not hold much information. More bits can be joined to form a number that can express larger numbers. With a total of n bits 2^n different numbers can be expressed. Yet this alone does not describe how a number can be represented in digital form. There are several number systems with different capabilities and short-comings
![[TOC]](PIC/toc.gif)
![[TOP]](PIC/up.gif)
The binary number systems are the most widely used number systems because of their simplicity. The basic binary number system is much similar to the decimal system we use. An n-bit number in the binary number system is an ordered sequence of bits:
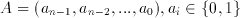 (2.1)
(2.1)
This number exactly represents an integer or fixed-point number. If we consider only natural numbers, a direct representation would be possible. This is called an unsigned binary number representation. For a set of a(i) the corresponding value can be calculated as:
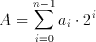 (2.2)
(2.2)
Numbers from 0 to 2^n-1 can easily be represented this way. If negative numbers are involved, a different approach needs to be taken. A solution analogous to the solution used in a decimal number system would be to use a digit to represent the sign. This representation, where the Most Significant Bit (MSB) of the sequence represents the sign of the number, is called the Sign-Magnitude Binary Number system. The value of A can be determined by:
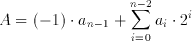 (2.3)
(2.3)
Although this format is relatively easy to comprehend, it has some important disadvantages. The number 0 can be represented in two different ways (one with a positive and one with a negative sign). A more significant problem is that positive numbers and negative numbers have to be treated differently in arithmetic operations. This is a major problem for operations that involve more than two operands, as the number of possibilities for the signs increase dramatically with the increasing number of operands.
The Two's Complement representation of the binary number system is the more frequently preferred alternative to represent both positive and negative numbers. The value of A of a two's complement number can be calculated by the following method:
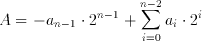 (2.4)
(2.4)
The negative value of any number with this representation can be calculated as:
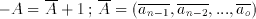 (2.5)
(2.5)
The most interesting feature of this representation is that for most of the basic arithmetic operations, digital computation blocks (with slight limitations) will perform correctly independent of the sign of the number. Table 2.1 gives all the combinations of a 4-bit number and lists their respective values for the three representations.
Table 2.1:Values of a 4-bit number according to its representation.
Bit sequence Unsigned Sign-Magnitude Two's Complement
0000 0 +0 0
0001 1 1 1
0010 2 2 2
0011 3 3 3
0100 4 4 4
0101 5 5 5
0110 6 6 6
0111 7 7 7
1000 8 -0 -8
1001 9 -1 -7
1010 10 -2 -6
1011 11 -3 -5
1100 12 -4 -4
1101 13 -5 -3
1110 14 -6 -2
1111 15 -7 -1
![[TOC]](PIC/toc.gif)
![[TOP]](PIC/up.gif)
The most important disadvantage of the binary number representation is that for some small change in value, a large number of bits within the number may change. As an example for a 8 bit number, consider the representation of 63 (0011 1111) and 64 (0100 0000) (notice that this example is independent of the number representation). Although the distance between these two numbers is only one LSB, 7 out of 8 digits have changed their values.
The Gray number system is a non-monotonic representation where two consecutive numbers differ in only one of their digits. For some applications such as counters or low-power address bus decoders the Gray number system can help reduce the power consumption as for consecutive numbers there will be fewer transitions (and associated power consumption).
The main disadvantage of this number representation is that it is not well suited for arithmetic operations mainly because Gray numbers are non-monotonic. The lower power consumption issue is also arguable, as the extra power used for the generation of Gray numbers may decrease the aforementioned power savings considerably [4].
![[TOC]](PIC/toc.gif)
![[TOP]](PIC/up.gif)
Addition is by far the most important elementary operation with in digital systems. The main difficulty with the addition lies in the carry problem (also referred as the curse of carry) [1]. The result of an operation on the bits of same magnitude can affects the result of higher order bits and is likewise affected by the result of lower order bits.
The redundant number systems are a result of this problem. The main idea is to represent one digit with more than one bits (hence the name redundant) to avoid carry propagation in adders. As a result of redundant bits, a number represented in a redundant number system has higher storage requirements than that of a number represented in a non-redundant form. A second disadvantage is that the conversion from a redundant number system to non-redundant number system is quite complicated.
![[TOC]](PIC/toc.gif)
![[TOP]](PIC/up.gif)
All the number systems discussed so far are so-called fixed point number systems. The floating point representation consists of a sign bit (S), a mantissa (M) and an exponent (E) in the form of:
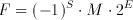 (2.6)
(2.6)
Table 2.2 shows two IEEE standarts for floating point representations.
Table 2.2 IEEE Floating point standart.
Standart n M bits E bits Range Precision single 32 23 8 3.8E+38 1E-7 double 64 52 11 9.0E+307 1E-15
Floating point operations require different operations for mantissa and exponent parts of the number. General purpose processors which are used for scientific computing make use of floating point arithmetics by means of dedicated Floating Point Units (FPU) to speed up computation intensive applications. Not more than five years ago these FPU's were usually auxiliary processors. Today all of the modern general purpose processors have embedded FPU blocks.
There are other number representations such as: Residue Number System, Logarithmic Number System and Anti-Tetrational Number System [5] whose details are beyond the scope of this text.
![[TOC]](PIC/toc.gif)
![[TOP]](PIC/up.gif)
Once the data is represented in digital form, it can be processed with a large number of algorithms. Any specialized hardware that performs signal processing on digitally represented data can be called Digital Signal Processing Hardware (DSP hardware). Few different families of DSP Hardware can be identified [1]:
DSP processors:
These chips are essentially RISC architecture processors
with specialized hardware for DSP algorithms. They can be programmed
to perform a wide range of algorithms.
DSP cores:
These blocks are large macro-blocks with the functionality
of a DSP processor that can be embedded in ASIC's. These cores would
include a more specialized hardware for the algorithm.
Application Specific DSP Chips:
These chips are designed for a specific
algorithm and are used where programmable approaches can not achieve
the required performance.
The nature of DSP algorithms have different requirements than generic computational algorithms. Multipliers and adders are indispensable blocks of any DSP algorithm. DSP algorithms operate on a fixed rate of data, putting strict restrictions on the speed of individual operations.
Another interesting aspect of DSP algorithms is that it frequently relies on the current as well as previous values of data. The only way to realize this is to use storage elements (registers or RAM). RAM access is a slow and complicated process and large memory arrays are the least wanted blocks in any high speed design. As an example, a (512 x 512), 8-bit grayscale image needs a storage of approximately 2 million bits which, in turn, requires a considerable RAM capacity. No DSP algorithm can afford to have simultaneous access to all pixels of this image, it can at most concentrate on one part of the image.
The main problem however, lies in the I/O bandwidth. The source that will provide the data to the DSP block and the receiving end that will receive the processed data, typically have limitations on the available bandwidth.
The introduction of DSP specific hardware dates back to the early 80's. First programmable DSP processors were mainly used for audio-band applications. Especially the Texas Instruments 320c series of general purpose DSP processor was widely used for a wide range of applications. Strangely enough, contrary to the parallel developments in general purpose microprocessors or memory chips, the DSP specific hardware did not have a continuously expanding usage within the 80's. It took almost 10 years until the developments in electronics industry enabled DSP hardware to be developed that were fast enough for image processing. Image filtering, compression and coding are the three main fields for which a number of dedicated chipsets have been produced.
![[TOC]](PIC/toc.gif)
![[TOP]](PIC/up.gif)
The last decade has seen an enormous increase in the capabilities and application areas of general purpose microprocessors. As a result of these developments, the average home computer user nowadays has a typical computation power which is at the same level of that of leading research institutes not much more than ten years ago. There are a few key reasons for this accelerated development [6]:
As a result, we are continuously offered an increasing number of extremely powerful general purpose processors which enable many sophisticated and computationally complex problems to be solved by software running on these processors. The main advantages of these processors are obvious:
At the beginning of 1980's when the first DSP chips were introduced to the market nobody would have believed that general purpose processors could outperform specialized Signal Processing Processors. The initial boom of DSP chips faded silently, and especially after the introduction of MMX extensions to the majority of general purpose processors (which essentially adds a number of specialized instructions for DSP), it is doubtful whether or not they can reconquer the market. While the future of DSP processors is not very bright, specialized DSP chips, and macro-blocks will continue to be play an important role in the future.
![[PREV]](PIC/back.gif)
![[TOC]](PIC/toc.gif)
![[TOP]](PIC/up.gif)
![[NEXT]](PIC/fwd.gif)
 KGF
KGF