

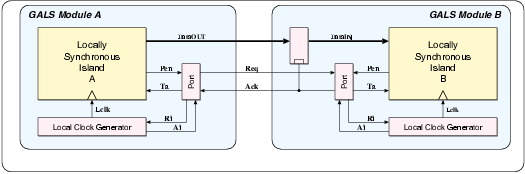
| (2.1) |
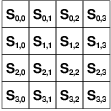
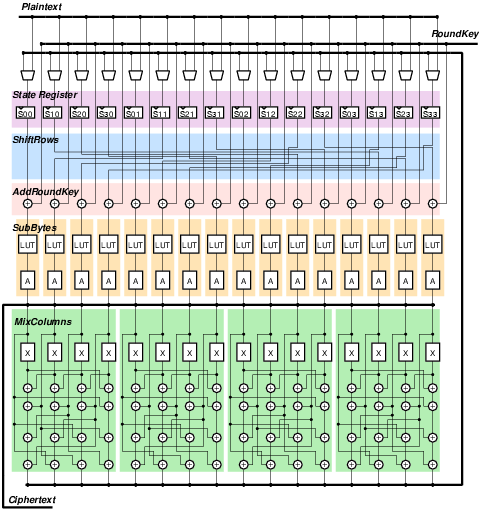
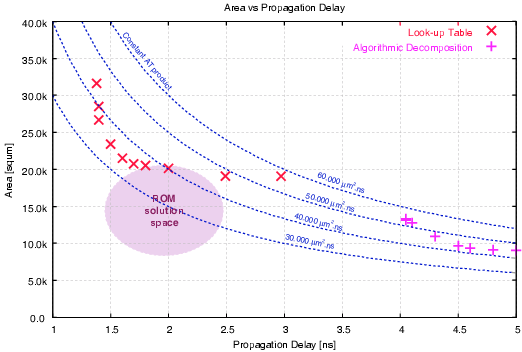
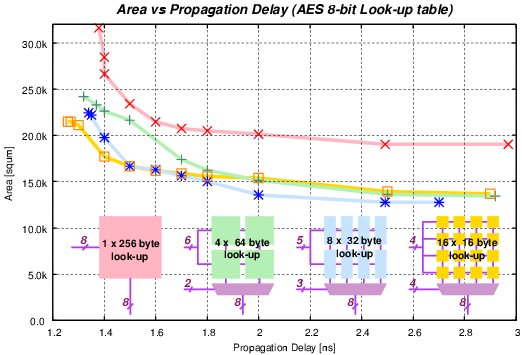
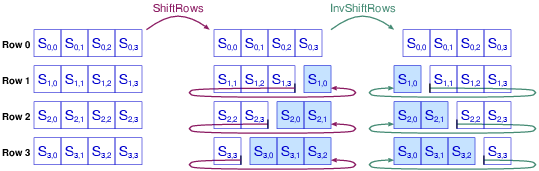
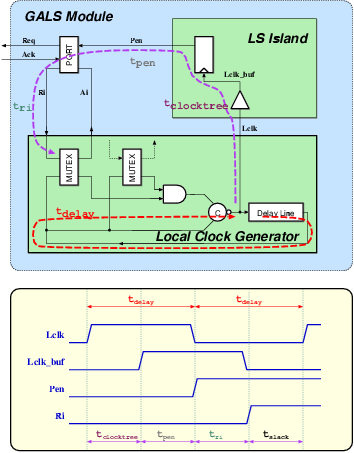
|
|
|
|
| Datapath Width | 8-bit | 16-bit | 32-bit | 64-bit | 128-bit |
| Parallel SubBytes units | 1 | 2 | 4 | 8 | 16 |
| Complexity (gate equivalents) | 5,052 | 6,281 | 7,155 | 11,628 | 20,410 |
| Area (normalized) | 1 | 1.266 | 1.472 | 2.432 | 4.269 |
| Clock cycles for AES-128 | 160 | 80 | 40 | 20 | 10 |
| Critical Path (normalized) | 1.349 | 1.341 | 1.206 | 1.133 | 1 |
| Total time for AES-128 (normalized) | 21.580 | 10.729 | 4.825 | 2.227 | 1 |
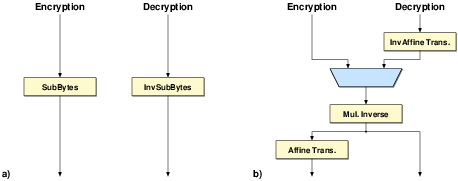
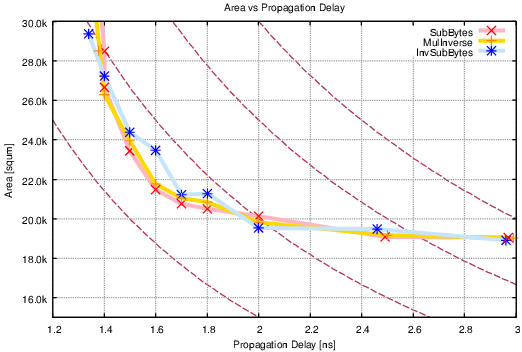
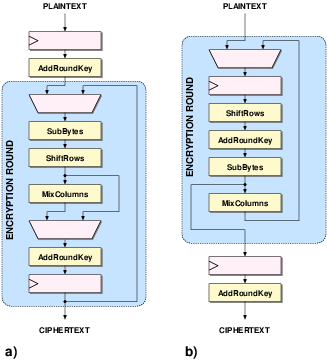
| Verbauwhede [VSK03] | Kim [KMB03] | Satoh [SMTM01] | Su [SLHW03] | Lu [LT02] | Ichikawa [IKM00] | |
| Technology | 0.18 m | 0.18 m | 0.11 m | 0.25 m | 0.25 m | 0.35 m |
| Area | 3.96 mm2 | N/A | 0.205 mm2 | 1.62 mm2 | N/A | N/A |
| Gate Equivalents | 173,000 | 28,626 | 21,337 | 63,400 | 31,957 | 612,834 |
| RAM | - | 4Kb | - | 4Kb | - | - |
| ROM | - | 128Kb | - | - | - | - |
| Throughput | 1600 Mb/s | 1640 Mb/s | 2600 Mb/s | 2970 Mb/s | 610 Mb/s | 1950 Mb/s |
| En/Decryption | encryption | both/shared | both | both | both/shared | both |
| Modes | all | ECB | ECB/CBC | ECB | ECB | ECB |
| Key Generation | on-the-fly | stored | on-the-fly | stored | on-the-fly | stored |
| Key Lengths | 128/192/256 | 128/192/256 | 128 | 128/192/256 | 128 | 128 |
| Datapath | 256-bit | 256-bit | 128-bit | 128-bit | 128-bit | 128-bit |
| Notes | supports 256-bit data | supports 256-bit data | synthesis results | pipelined | synthesis results | unrolled rounds synthesis results |
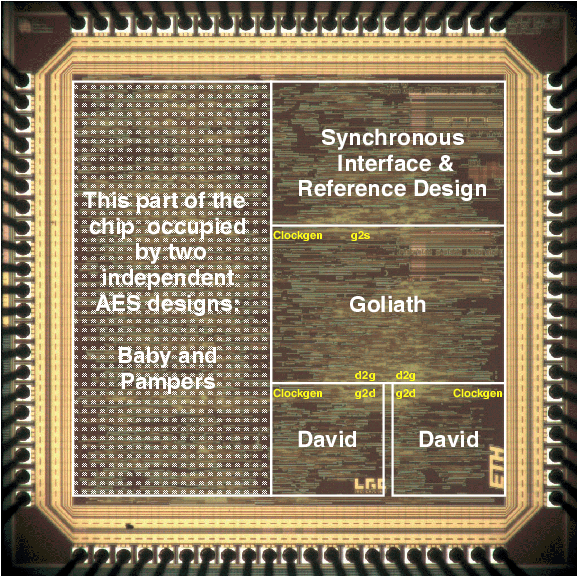
| Riddler [LTG+02] | Fastcore [GBG+04] | Ares [PGH+04] | Baby | Pampers | Acacia | |
| Technology | 0.6 m | 0.25 m | 0.25 m | 0.25 m | 0.25 m | 0.25 m |
| Area | 37.8 mm2 | 3.56 mm2 | 1.2 mm2 | 0.35 mm2 | 0.58 mm2 | 1.1 mm2 |
| Gate Equivalents | 75,000 | 119,000 | 42,408 | 14,259 | 23,076 | 39,012 |
| RAM | - | - | - | - | - | 2Kb |
| ROM | - | - | - | - | - | - |
| Throughput | 2160 Mb/s | 2120 Mb/s | 1150 Mb/s | 285 Mb/s | 230 Mb/s | 180 Mb/s |
| En/Decryption | both/shared | concurrent | encryption | encryption | encryption | both/shared |
| Modes | ECB | all | ECB/OFB | ECB/OFB | ECB/OFB | ECB |
| Key Generation | stored | on-the-fly | on-the-fly | on-the-fly | on-the-fly | stored |
| Key Lengths | 128 | 128/192/256 | 128 | 128/192/256 | 128/192/256 | 128/192/256 |
| Datapath | 2 x 128-bit | 128-bit | 128-bit | 16-bit | 16-bit | 2 x 16-bit |
| (3.3) |
| (3.4) |
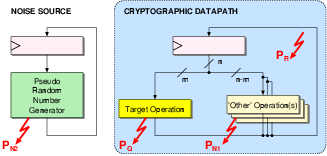
|
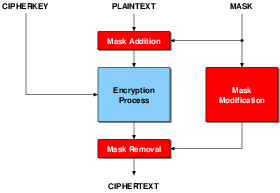
| (3.6) |
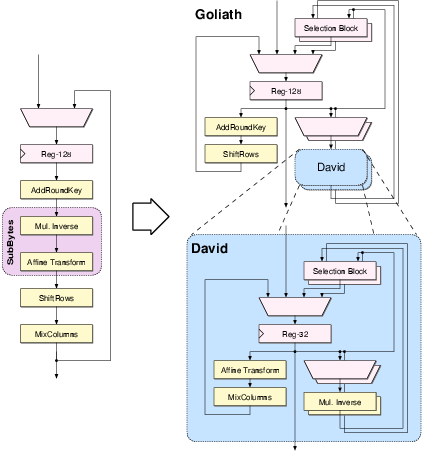
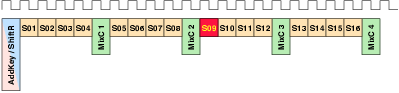


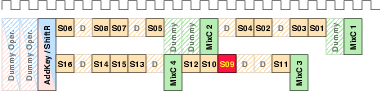
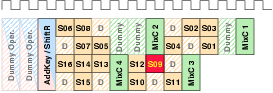
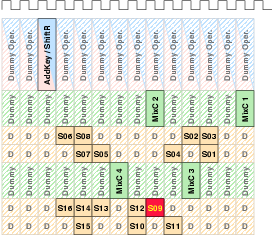
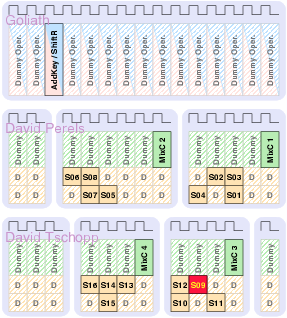
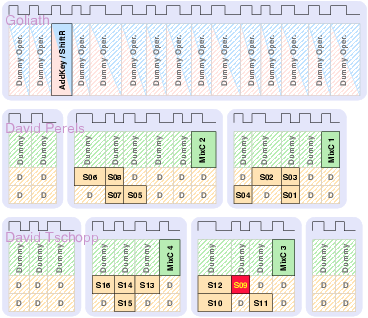
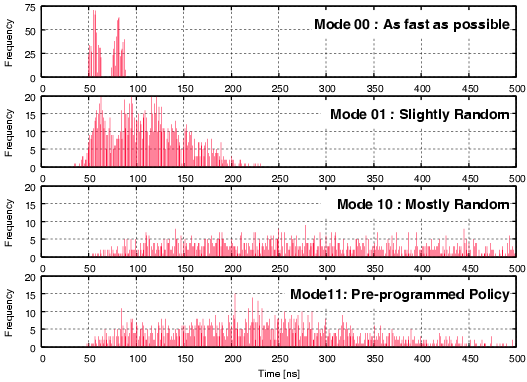
| Mode | Description | Run time [ns] | norm. |
| 00 | As fast as possible | 114,400 | 1 |
| 01 | Using slightly random countermeasures | 165,320 | 1.44 |
| 10 | Using highly random countermeasures | 616,240 | 5.38 |
| 11 | Using pre-programmed policy | 203,840 | 1.78 |
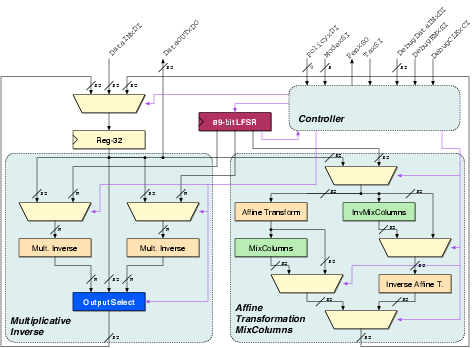
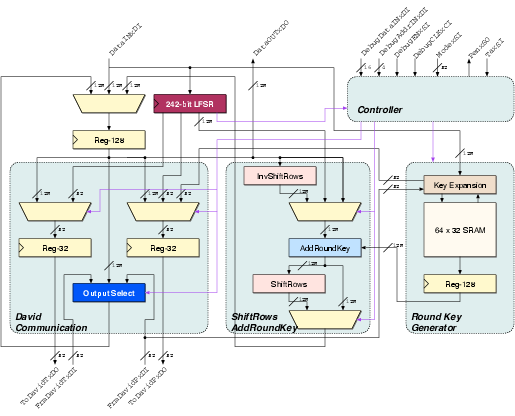
| (4.1) |
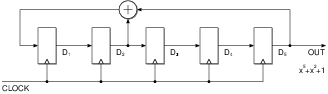
| Initial | D1 | D2 | D3 | D4 | D5 |
| P(x) | D2ÅD5 | D1 | D2 | D3 | D4 |
| P(x)2 | D1ÅD4 | D2ÅD5 | D1 | D2 | D3 |
| P(x)3 | D2ÅD3ÅD5 | D1ÅD4 | D2ÅD5 | D1 | D2 |
| P(x)4 | D1ÅD2ÅD4 | D2ÅD3ÅD5 | D1ÅD4 | D2ÅD5 | D1 |
| P(x)5 | D1ÅD2ÅD3ÅD5 | D1ÅD2ÅD4 | D2ÅD3ÅD5 | D1ÅD4 | D2ÅD5 |
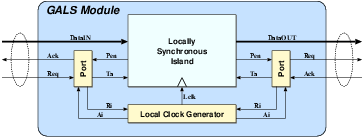
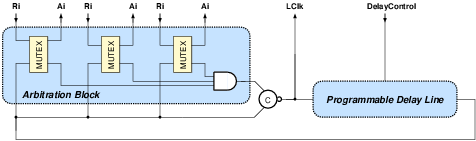
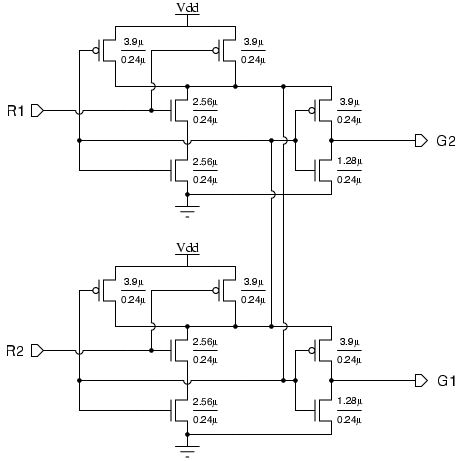
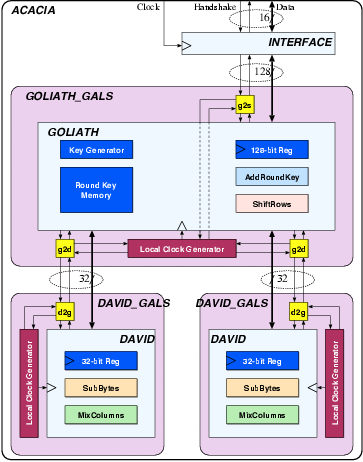
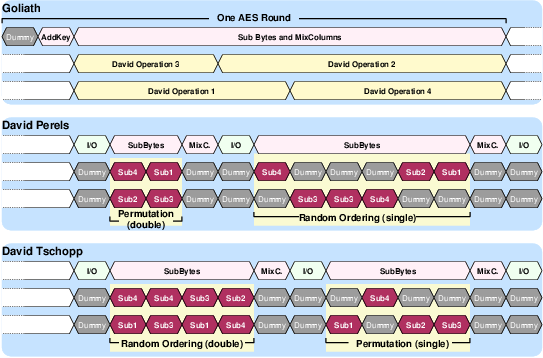
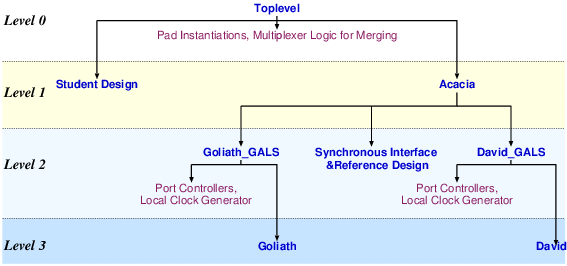
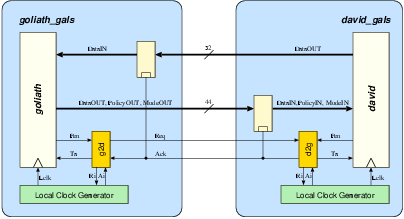
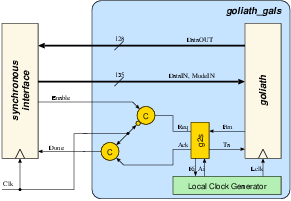
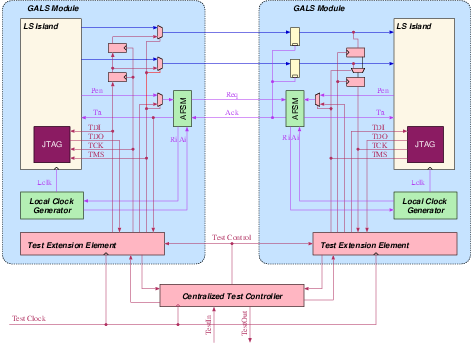
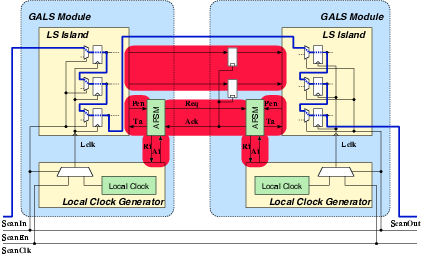
| Synchronous | GALS + DPA | |||
| Matthias | Schoggi | David | Goliath | |
| Area (m2) - LS | 93,123 | 207,031 | 183,007 | 551,194 |
| Area (m2) - ClockGen | N.A. | N.A. | 7,579 | 7,626 |
| Area (m2) - Ports | N.A. | N.A. | 6,225 | 11,412 |
| Area (m2) - TOTAL | 393,277 | 963,855 | ||
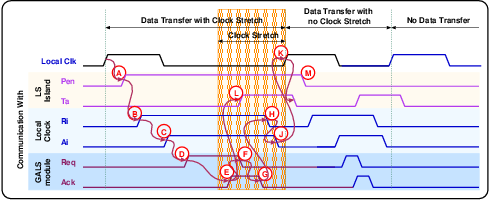
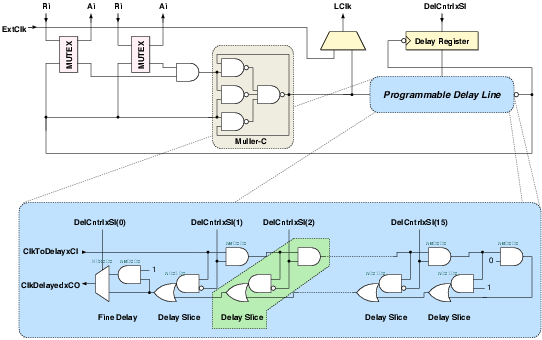
| Critical path (ns) | 5.43 | 5.84 | 3.98 | 5.27 |
| Latency (cycles) | 3 | 1 | 4 | 2 |
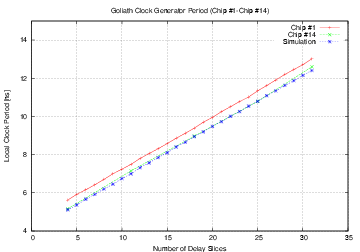
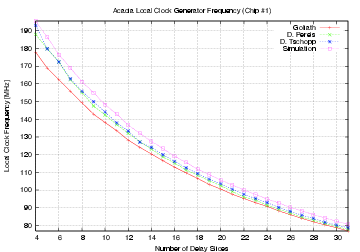
| Clock frequency (MHz) | 170.96 | 250.8 | 189.6 | |
| Encryption round (cycles) | 7 | 8 | 2 | |
| Encryption round (ns) | 40.88 | 42.38 | ||
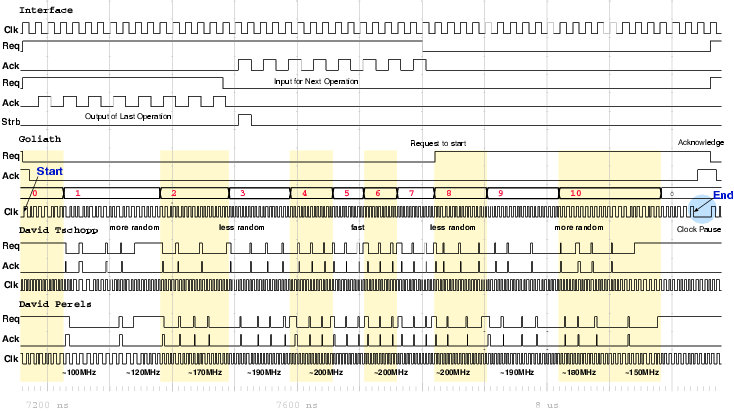
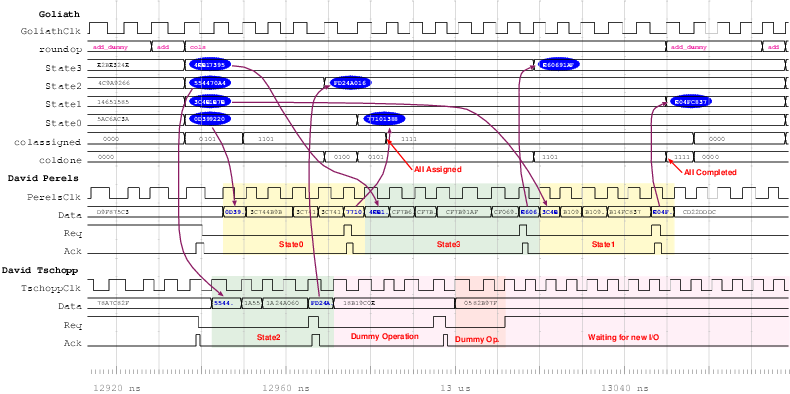
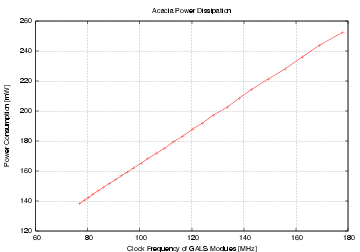
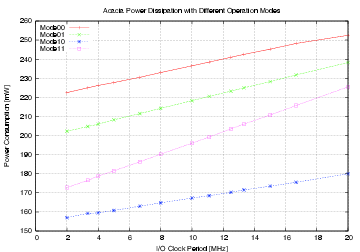
| Mode | Clock | Number of | Max. Time | Throughput | Energy |
| [MHz] | Cycles | [ns] | [Mb/s] | [mJ/Mb] | |
| Acacia - 00 | 50 | 36 | 720.0 | 177.7 | 1.232 |
| Acacia - 01 | 50 | 44 | 880.0 | 145.4 | 1.362 |
| Acacia - 10 | 50 | 112 | 2,440.0 | 57.1 | 2.704 |
| Acacia - 11 | 50 | 46 | 920.0 | 139.1 | 1.198 |
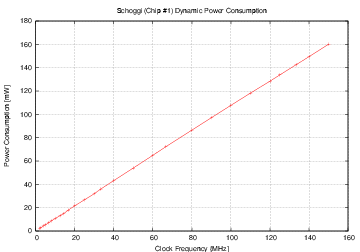
| Schoggi | 150 | 117 | 779.2 | 164.2 | 0.976 |
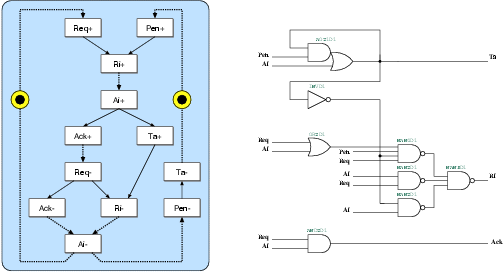
| (5.1) |
| Description | bits | value |
| quantities | ||
| a million | 20 | 1·106 |
| number of AES encryptions that can be calculated per second using the fastest Pentium processor | 24 | 20·106 |
| number of processors that can be powered by one nuclear reactor | 25 | 40·106 |
| number of people living in the world | 32.5 | 6.5·109 |
| number of processors that can be powered by the total amount of energy consumed in the world | 39 | 500·109 |
| number of floating point operations calculated by the fastest supercomputer of the world each second (as of June 2005) | 47 | 136·1012 |
| number of atoms in a drop of water | 73 | 10·1021 |
| number of processors that can fill all oceans of the world | 78 | 323·1021 |
| number of processors that can be powered by the sun | 84 | 16·1024 |
| number of atoms in a human body | 92.5 | 7·1027 |
| number of atoms in planet earth | 166.5 | 133·1048 |
| time spans | ||
| seconds in a year | 25 | 31.5·106 |
| average life of man in seconds | 31 | 2.4·109 |
| written history in seconds | 37.5 | 189·1012 |
| age of the world in seconds | 57 | 145·1015 |
| age of the universe in seconds | 59 | 630·1015 |
|
|
|
|
|
|