

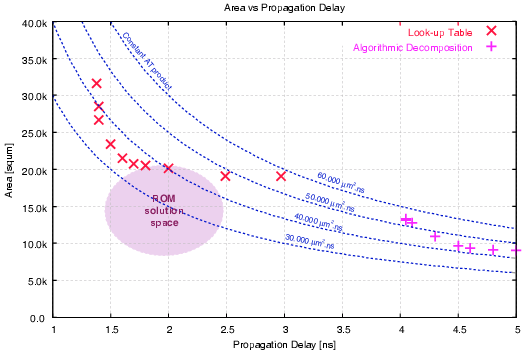
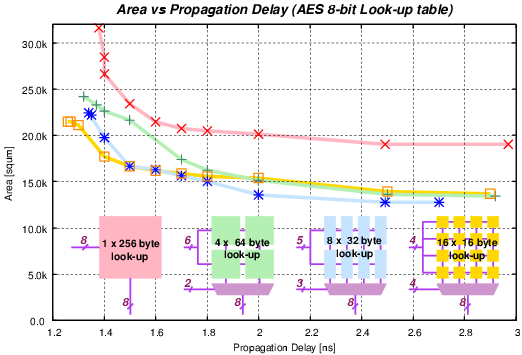
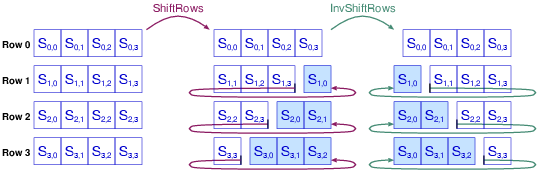
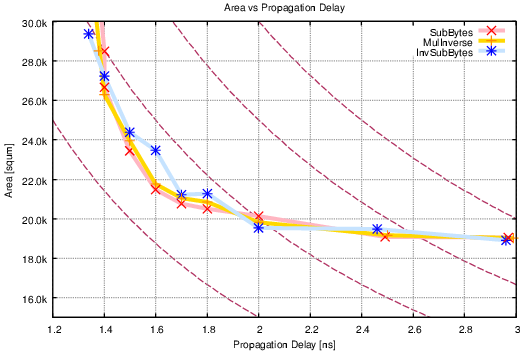
|
|
|
|
| Datapath Width | 8-bit | 16-bit | 32-bit | 64-bit | 128-bit |
| Parallel SubBytes units | 1 | 2 | 4 | 8 | 16 |
| Complexity (gate equivalents) | 5,052 | 6,281 | 7,155 | 11,628 | 20,410 |
| Area (normalized) | 1 | 1.266 | 1.472 | 2.432 | 4.269 |
| Clock cycles for AES-128 | 160 | 80 | 40 | 20 | 10 |
| Critical Path (normalized) | 1.349 | 1.341 | 1.206 | 1.133 | 1 |
| Total time for AES-128 (normalized) | 21.580 | 10.729 | 4.825 | 2.227 | 1 |


| Verbauwhede [VSK03] | Kim [KMB03] | Satoh [SMTM01] | Su [SLHW03] | Lu [LT02] | Ichikawa [IKM00] | |
| Technology | 0.18 m | 0.18 m | 0.11 m | 0.25 m | 0.25 m | 0.35 m |
| Area | 3.96 mm2 | N/A | 0.205 mm2 | 1.62 mm2 | N/A | N/A |
| Gate Equivalents | 173,000 | 28,626 | 21,337 | 63,400 | 31,957 | 612,834 |
| RAM | - | 4Kb | - | 4Kb | - | - |
| ROM | - | 128Kb | - | - | - | - |
| Throughput | 1600 Mb/s | 1640 Mb/s | 2600 Mb/s | 2970 Mb/s | 610 Mb/s | 1950 Mb/s |
| En/Decryption | encryption | both/shared | both | both | both/shared | both |
| Modes | all | ECB | ECB/CBC | ECB | ECB | ECB |
| Key Generation | on-the-fly | stored | on-the-fly | stored | on-the-fly | stored |
| Key Lengths | 128/192/256 | 128/192/256 | 128 | 128/192/256 | 128 | 128 |
| Datapath | 256-bit | 256-bit | 128-bit | 128-bit | 128-bit | 128-bit |
| Notes | supports 256-bit data | supports 256-bit data | synthesis results | pipelined | synthesis results | unrolled rounds synthesis results |
| Riddler [LTG+02] | Fastcore [GBG+04] | Ares [PGH+04] | Baby | Pampers | Acacia | |
| Technology | 0.6 m | 0.25 m | 0.25 m | 0.25 m | 0.25 m | 0.25 m |
| Area | 37.8 mm2 | 3.56 mm2 | 1.2 mm2 | 0.35 mm2 | 0.58 mm2 | 1.1 mm2 |
| Gate Equivalents | 75,000 | 119,000 | 42,408 | 14,259 | 23,076 | 39,012 |
| RAM | - | - | - | - | - | 2Kb |
| ROM | - | - | - | - | - | - |
| Throughput | 2160 Mb/s | 2120 Mb/s | 1150 Mb/s | 285 Mb/s | 230 Mb/s | 180 Mb/s |
| En/Decryption | both/shared | concurrent | encryption | encryption | encryption | both/shared |
| Modes | ECB | all | ECB/OFB | ECB/OFB | ECB/OFB | ECB |
| Key Generation | stored | on-the-fly | on-the-fly | on-the-fly | on-the-fly | stored |
| Key Lengths | 128 | 128/192/256 | 128 | 128/192/256 | 128/192/256 | 128/192/256 |
| Datapath | 2 x 128-bit | 128-bit | 128-bit | 16-bit | 16-bit | 2 x 16-bit |
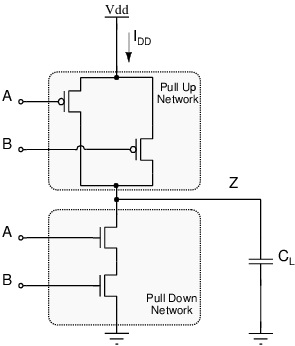
| (3.3) |

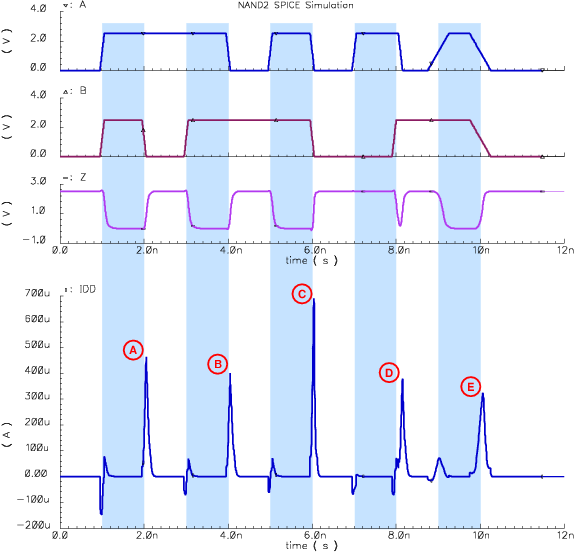
| (3.4) |
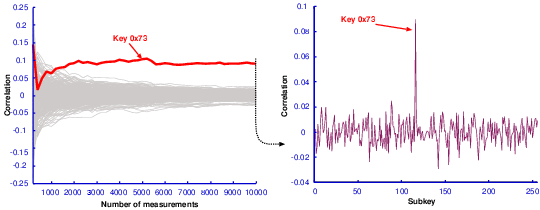
|
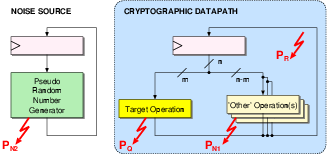
| (3.6) |